NOT: Alan dinamik fizik, dolayısıyla verilen bu kuvvetin mantığına olta atıp bir şeyler sezmeyi hedefliyoruz daha ötesini değil.
İhmaller kabul edilerek verilen öncevap:
Vericeğim teori şunu söylüyor, gezegenlere evrenin hertarafından her an etkı eden bır kuvvet,i.e.(yani), bir itici dalga kuvveti olsun.
Eğer gezegenlerin yakınlarında cisimler yok ise hertaraftan gelen dalga kuvvetleri o gezegeni dengede tutar.

Eğer gezegenin yakınında bir engelleyici cisim var ise, gezegene göre bulunduğu konumdan dolayı, cisimin engellediği bölgeden dalga kuvveti gelmez ve cisim ters yönde itilir.
Peki bu aksiyomlar, $\mathcal {\overrightarrow F}=G\frac{m_1m_2}{(d_{_{m_1-m_2}})^2}$ ile uyuşuyor mu?
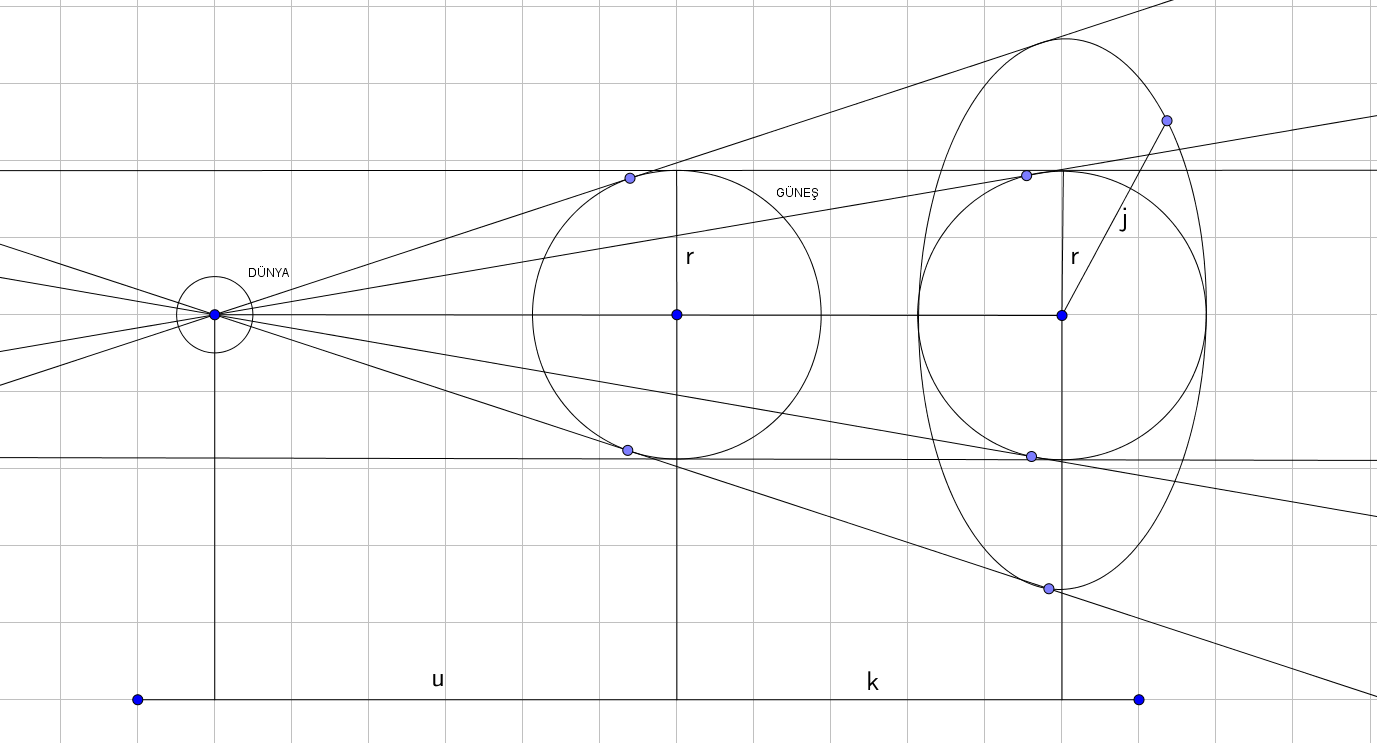
Elimden geldiğince sade yazmaya çalıştım. Yukardaki durumda engellenen alanları dolayısıyla kuvvetin nasıl değiştiğini göstermek için alanlar çizilmiştir.
$j$ yarıçaplı konik cisim aslında bir küredir ama engellediği alan Dünyaya göre bir kesit alanı olacağından eliptik gibi çizilmesi gerekti burada görüldüğü üzre Güneşlere, Dünyadan çizilen teğet doğrular tam bir dik yarıçap oluşturmadığından bu çözüm ana çözüme göre daha basit olucaktır.
Eğer teorim doğru ise engellenen alan ile kuvvet lineer olarak doğru orantılı ve merkezler arası yarıçap ile ters orantılı olmak zorunda.
Güneş $u$ kadar yakındayken ve $u+k$ kadar yakındayken durumları yukarıda resmedilmişti, dolayısıyla bu $2$ durumu karşılaştırmak için bana ortak bir alan gerek bu ortak alan da, Güneşin $u+k$ uzaklıktaki durumu.(Neden böyle olduğu düşünülmeli ve aşşağıdaki durum göz önüne alınmalıdır.)

Bu durumdan dolayı;
$j=\left(\dfrac{u+k}{u}\right)r$ olur.
Güneş $u$ kadar uzaktayken, $\mathcal {\overrightarrow F_{(u)}}=G\frac{m_Dm_G}{u^2}$ ve engellenen alan sağ taraf için $\pi j^2=\pi \left(\dfrac{u+k}{u}\right)^2 r^2$ olur.
Güneş $u+k$ kadar uzaktayken, $\mathcal {\overrightarrow F_{(u+k)}}=G\frac{m_Dm_G}{(u+k)^2}$ ve engellenen alan sağ taraf için $\pi r^2$ olur.
Teori doğru ise kuvvetler ve alanlar oranı birbirine eş çıkmalı.
$\dfrac{\overrightarrow F_{(u)}}{\overrightarrow F_{(u+k)}}=\dfrac{G\frac{m_Dm_G}{u^2}}{G\frac{m_Dm_G}{(u+k)^2}}=\dfrac{\pi \left(\frac{u+k}{u}\right)^2 r^2}{\pi r^2}$
$\Box$
Ancak teorinin çalışmadığı ters örnek vardır şöyleki;
Hacmi eşit,kütlesi farklı $2$ tane Güneş alır ve ayrı ayrı dünyanın yanına aynı uzaklıktaki merkezlere koyarsak kütlesi fazla olan güneş dünyayı daha çok çekmesi gerekirken bu teoriye göre hacim aynı olduğundan eşit olmalıdır ve hatalıdır.
Tabi bu çelışki, yoğunluk rötuşu ile düzeltilebilir, ilerde bunu genelleştirebiliriz.