Duzenleme: Sayilari biraz arastirinca suraya cikti yol.
$a(n,k)=(k-1)^n + (-1)^n (k-1)$ dizisi cevap olmus oluyor.. Acikcasi binomlu formul bekliyordum, bu ne lan..
Ilk cevap:
Acik formul goremedim henuz ama deneysel olarak sunlari yapabiliriz. Satirlar boya sayisi $k$'yi ve sutunlar dilim sayisi $n$'yi gostersin.
Mathematica kodu.
s = 7;
sol[k_, n_] :=
With[{list = Flatten@Take[Transpose@ConstantArray[Range@s, s], k]},
perm = Permutations[list, {n}];
Length@Complement[perm,
Flatten[{Table[
Select[perm, #[[i]] == #[[i + 1]] &], {i, n - 1}], {Select[
perm, #[[1]] == #[[-1]] &]}}, 2]]]
TableForm[Table[sol[k, n], {k, s}, {n, s}],
TableHeadings -> {Range@s, Range@s}]
$
\begin{array}{c|ccccccc} &1&2 & 3 & 4 & 5& 6& 7 &\\\hline
1&0 & 0 & 0 & 0 & 0 & 0 & 0 \\
2&0 & 2 & 0 & 2 & 0 & 2 & 0 \\
3&0& 6 & 6 & 18 & 30 & 66 & 126 \\
4&0 & 12 & 24 & 84 & 240 & 732 & 2184 \\
5& 0& 20 & 60 & 260 & 1020 & 4100 & 16380 \\
6& 0 & 30 & 120 & 630 & 3120 & 15630 & 78120 \\
7&0 & 42 & 210 & 1302 & 7770 & 46662 & 279930 \\
\end{array}
$
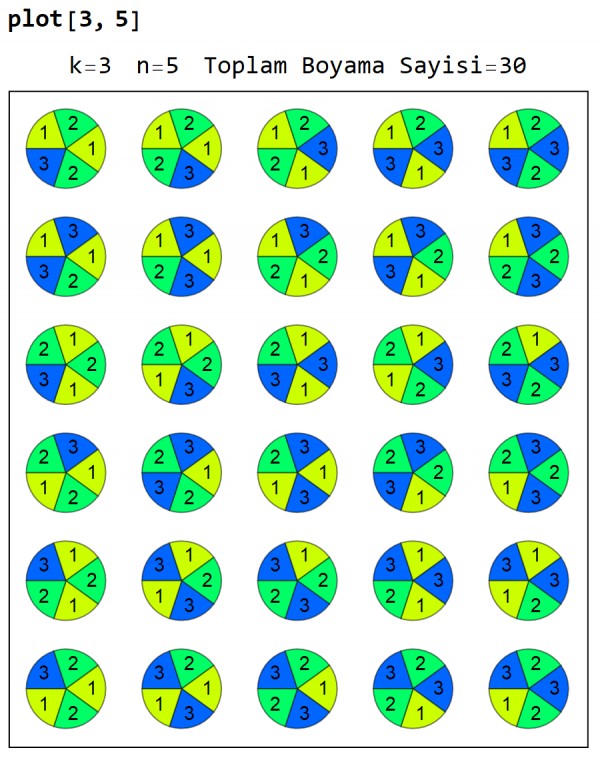
Bazi ornekleri cizelim.
plot[k_, n_] :=
With[{list = Flatten@Take[Transpose@ConstantArray[Range@k, k], k]},
perm = Permutations[list, {n}];
r = Complement[perm,
Flatten[{Table[
Select[perm, #[[i]] == #[[i + 1]] &], {i, n - 1}], {Select[
perm, #[[1]] == #[[-1]] &]}}, 2]];
data = Transpose /@
Table[{ToString /@ r[[i]], ConstantArray[1, n]}, {i, Length@r}];
colors = Thread[ToString /@ Range@k -> Take[Hue /@ (Range[5]/5), k]];
fig = PieChart[#[[All, 2]], ChartStyle -> #[[All, 1]] /. colors,
ChartLabels -> #[[All, 1]], ImageSize -> 50] & /@ data;
Labeled[
Framed[Multicolumn[fig, {Automatic, 14},
Appearance -> "Horizontal"]],
Row[{"k=" <> ToString@k,
"n=" <> ToString@n,
"Toplam Boyama Sayisi=" <> ToString@Length@fig}, Spacer[6]],
Top]]