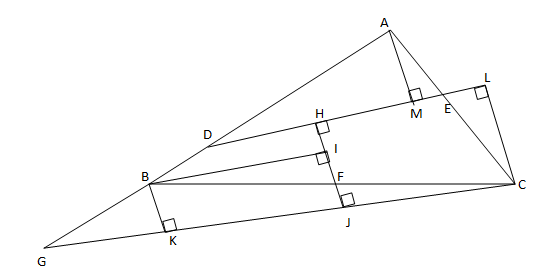
$[AB]$ ve $C$'den $[DE]$'ye paralel olacak şekilde çıkan doğru parçası üçgen dışında bir $G$ noktasında kesişsinler.
$[HJ] \perp [GC]$ ve $[BK]\perp [GC]$ olsun.
$C$'den $[DE]$'ye inilen dikme ayağı $L$ ve $A$'dan $[DE]$'ye inilen dikme ayağı $M$ olsun. $|MA|=|LC|=h$ olsun.
$B$'den $[HF]$'ye inilen dikme ayağı $I$ olsun. $|IF|=|FJ|=h-4$
$BKC \equiv FJC \rightarrow |BK|=2h-8$
$|DE|=x$ olsun.
$ABC \equiv AGC \rightarrow |GC|=2x$
$A(ABC)=A(AGC)-A(BGC)=\frac{(|MA|+|CL|)|GC|}{2}-\frac{|BK||GC|}{2}=\frac{2h.2x}{2}-\frac{(2h-8)2x}{2}= \\ = 8x=48 \rightarrow x=6$