Momentum korunumu eğer var ise aşağıdaki 2 şart sağlanmalıdır.
$A:$ Çarpışma anını kuvvet toplamı şeklinde yazabilmeliyiz, yani, momentumların çarpışma anındaki durumunu, cisimler hareket kazanırken uygulanan kuvvetlerin bileşkelerin toplamı şeklinde yazabilmeliyiz.
$B:$ Sistemi eylemsizlikten, hareket haline geçiren FAKTÖR, çarpışma sonrası hareket durumundan, eylemsizlik durumuna geçiren faktörle aynı ise momentum korunur.
$A:$ Çarpışma anını kuvvet toplamlarına ayırmak için şunlar gerekli;
$ 1 :$ Cisimlerin çarpıştığı biliniyor ve çarpışırken sadece belli hızlara sahipler (Toplam etkiyen kuvvet $\displaystyle\sum \overrightarrow F=0$).
$ 2 : $ Eğer başlangıçta $2$ cisim de durağan ise bunlara belli bir kuvvet $t$ zamanı boyunca uygulanmış demektir.(Zaten nerdeyse her cisim, istenilen göreli sisteme göre, duruyor, sabit hızlı hareket ediyor veya ivmeleniyor olabilir.)
$ 3 : $ Fiziksel deneyimlerimizden biliyoruz ki bu çarpışma sonucunda yönler vektörel olarak hesaplanır ama vektörlerin gücünü bilmemize rağmen cisimlerin son vektörlerini şimdilik bilemiyoruz.
$ 4 :$ Cisimler $S$ göreli sisteminde durağanken $t$ zaman boyunca $F$ kuvvet etki edecek ve biliyorum ki $\displaystyle\int_{t_1}^{t_2} Fdt=P$ diye tanımlı ve bunun fiziksel oldugunu ispatlamak için integrallerde ortalama değer teoremini kullanacağız.
$ 5-a):$ Cisimler çarpışmadan sonra, hız kazandırılan kuvvetlerinin vektörlerinin bileşkesine göre yön alıyor. "Kaynak:Newtonun 2. yasası ve dolayısıyla 1. yasası"
$ 5-b):$ Çarpışma oluyor ise, kuvvetler kazandırılırken çarpışan cisimlerin kuvvet bileşimlerini alabilirim. "Kaynak:Sırasal Nedenselliğin, yukardaki 5-a) ya tersten uygulanması."
$ 5-c):$ Bunun için olağan durumu şöyle daha iyi anlayabiliriz.Çarpışma oluyor ve vektörel olarak oraya buraya gidiliyor bu gidişin vektörel olarak Momentum Korunumu olduğu biliniyor, gözlemlenmiş ve kabul edilmiş, ancak bunlara ihtiyaç olmadan da daha temel aksiyomlardan gidebiliriz.Dolayısıyla son durumdaki yön ve büyüklükleri nasıl analiz edeceğimize bakalım.
Not:
Fizik yapılırken genel ve kanunsal şeyler söylemek çok zor, tatmin edici ispatlar deliller göstemek daha zordur.Dolayısıyla elimizde ne var ise ne tanımlamışsak ve neyi amaçlıyorsak ona ulaşmak için tutarlı yollar inşaa edip kullanmalıyız.
Gerçek hacimli sistemler için çarpışma aşşağıdaki gibidir.
ŞEKİL-1
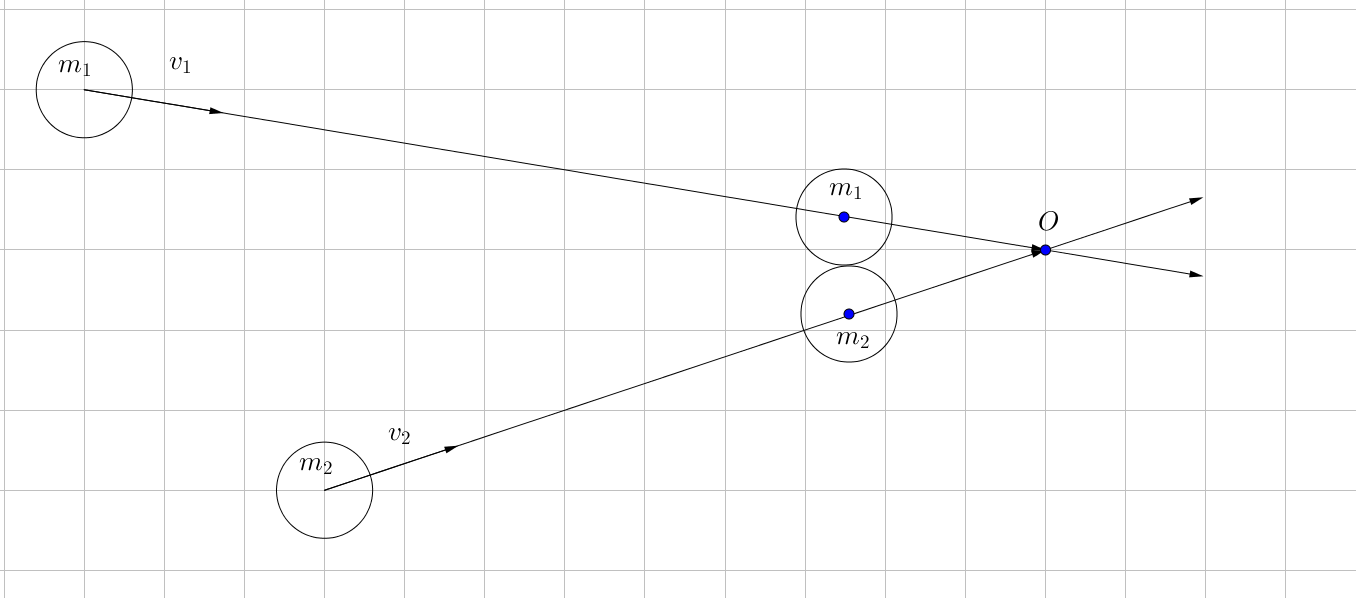
Hacimleri olan sistemleri tam teorik olarak doğru analiz etmek çok sorunlu olduğundan ve bize lazım olan bu işin temel mantığı olduğundan aşağıdaki model ile devam edelim.

ŞEKİL-2
Kütlenin korunum kanunundan dolayı kütleler değişmez, ama hızların "istisnalar haric" değiştiğini biliyoruz dolayısıyla cisimlerin ilk hızlarına $v_i$ son hızlarına ise $w_i$ ismini verdim.
Elimizde sadece hız var dolayısıyla $\triangle t$ süresi boyunca uygulanan kuvvet var, bunun üzerinden gidelim;
Tanım:
$\triangle=t_2-t_1,\quad(t_2>t_1)$
$\overrightarrow a:$ ivme
$m:$ kütle (göreceli olarak değişmiyor, her zaman sabit.)
$t:$ zaman.
$\overrightarrow F=m \overrightarrow a$
Momentum:$\displaystyle\int_{t_1}^{t_2} \overrightarrow F dt=m\overrightarrow v=\overrightarrow {P(t)}$
Bu ispat'ın temeli olarak yukarıdaki maddelerde anlatıldığı gibi "ŞEKİL-2" 'yi yeniden sembolize edersek;

ŞEKİL-3: Kuvvetleri ikişer kez kullandığımızdan her bir ayrık kuvvet bileşkesi $2avrg(F)$ oldu.
TEMEL ANLAM:
ÇARPIŞMA ANINDA MOMENTUMLAR BİRBİRİ ARASINDA ETKİLEŞİM GEÇİRİR, BUNUN TAM ANLAMI ŞUDUR, EĞER BEN BU MOMENTUMU, ZAMANA KUVVET OLARAK YAYARSAM VE O YAYDIGIM ZAMAN ARALIĞINDA ÇARPIŞMADA OLAN MOMENTUMU ANALIZ EDERSEM NE OLDUGUNU GÖREBİLİRİM.
İvme tanımlı olduğu aralıkta süreklidir dolayısıyla rieamann integrallenebilir.
$\overrightarrow a$(ivme),dolayısıyla $\overrightarrow F$(kuvvet) $[t_1,t_2]$ aralığında sürekli olduğundan $t_c\in[t_1,t_2]$ için ;
$avrg(F)=\overrightarrow F(t_c)=\dfrac{1}{t_2-t_1}\displaystyle\int_{t_1}^{t_2}\overrightarrow F(t)dt$ ,
Ve dolayısıyla $(t_2-t_1)avrg(F)=\displaystyle\int_{t_1}^{t_2}\overrightarrow F(t)dt=P$
İspat:
$\min \overrightarrow F\le \dfrac{1}{t_2-t_1}\displaystyle\int_{t_1}^{t_2}\overrightarrow F(t)dt \le \max \overrightarrow F$
Sürekli fonksiyonlar için ara değer teoreminden dolayı böyle bir max-min aralığında $F(t_c)$ bulunur. $\Box$
$B:$
Bu cisimler çarpışıyor ise ve başlangıç hızları $0$ ise aynı $\triangle t$ süresi boyunca $F_i$ kuvvetleri uygulayalım ve bileşkelerini alalım, buraya kadar yapılanlardan anlaşılcağı üzre, cisimler çarpışacagından ve vektörlerle çalıştığımızdan yönler hakkında endişelenmemize gerek yok.
Tüm sistemi eylemsizlikten ilk olarak harekete daha sonra çarpıştırmaya ve en son olarak tekrar eylemsizliğe çevirelim.
Eylemsizlikten harekete ilk geçiş, çarpışmadan sonraki durumdan eylemsizliğe geçiş ile aynı ise vektörel kuvvet ve momentum korunmuştur.
Ayrık olan toplanan kuvvetler, çarpışmadan sonraki durumu ifade eder;
$1-)$ Momentum tanımı, çarpışmadan önceki kuvvet toplamı;
$P_1+P_2=m_1v_1+m_2v_2=\displaystyle\int_{t_1}^{t_2}\left(\overrightarrow {F_1}(t)+\overrightarrow {F_2}(t)\right)dt=(t_2-t_1)\left[avrg(F_1)+avrg(F_2)\right]$
$2-)$ Momentumları ayrık kuvvet toplamlarıyla elde etme, çarpışma anı ve sonrası için kuvvet toplamı;
$P_1^{'}+P_2^{'}=m_1w_1+m_2w_2=\dfrac12\displaystyle\int_{t_1}^{t_2}\left(\overrightarrow {F_1}(t)+\overrightarrow {F_{21}}(t)\right)dt+\dfrac12\displaystyle\int_{t_1}^{t_2}\left(\overrightarrow {F_2}(t)+\overrightarrow {F_{12}}(t)\right)dt=(t_2-t_1)\left[avrg(F_1)+avrg(F_2)\right]$
$3-)$ Kuvvet toplamları gereği $1-)=2-)$ olur ve;
$\boxed{\boxed{\boxed{ m_1v_1+m_2v_2=m_1w_1+m_2w_2}}}$ $\Box.$
Enejinin korunup korunmaması ile ilgilenmedik bile.Sadece kuvvet ve kuvvetin yorumlanma şeklini algıladık.