Merhaba kısaca ve anlaşılır bir şekilde anlatmaya çalışacağım.
eğer bir fonksiyonun x a'ya yaklaşırken limiti L ise
0'dan büyük her epsilon için en az bir delta buluyoruz ve rastgele seçilecek x'in a'ya uzaklığı 0'dan büyük deltadan küçükse f(x) lerin de L'ye olan uzaklığı epsilondan küçük oluyor sonuç olarak epsilonla delta arasında bağıntı bulup genelleme yapabilmek için
deltayı epsilonun bir fonksiyonu olarak yazıp limitimizin ispatını yapmış oluyoruz
ama ben mantıken şöyle bi açıdan da düşündüm her epsilon için en az bir delta varsa
aynı zamanda her delta içinde en az bir epsilon olması gerekir
dolayısıyla deltayı epsilonun bir fonksiyonu olarak yazmak yerine
epsilonu deltanın bir fonksiyonu yazarak çözüm yapabilirmiyim diyerek düşünerek ispatlamaya çalıştım
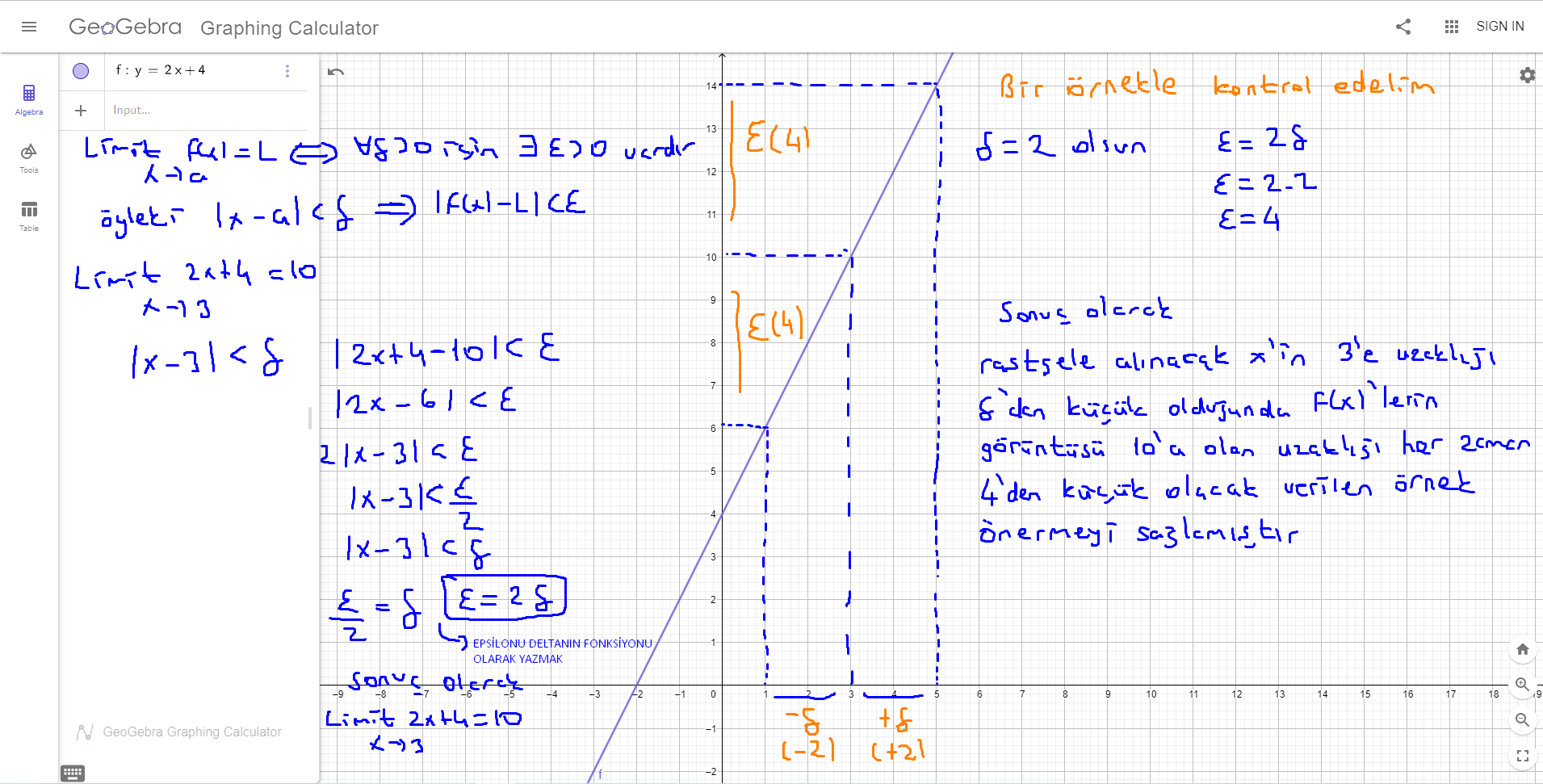
LateX bilmediğimden dolayı buraya işlemleri yazamadım şimdiden özür dilerim yaptığım işlemlerle ilgili bilgiler eklediğim fotoğrafta mevcuttur
Sonuç olarak eğer benim düşünceme katılmıyorsanız yazdığım önermeyi çürüterek veya aksini ispat eden en az bir örnek vererek kanıtlar mısınız?
eğer aşağıdaki resim bulanık gözüküyorsa resim linkini bırakıyorum
https://i.hizliresim.com/rjmjlxz.png