Evlere 1,2,3 çeşmelere A,B,C diyelim. Çizilebildiğini sayıp çelişki elde edeceğiz. Bu çelişkiyi bulmak için elementer olmayan (ileri lisans düzeyi) düzlemle (düzlemin topolojisi) ilgili teorem veya teoremlere gerek var.
Ben ispatı zor ama ifadesi kolay olan Jordan ın eğri Teoremini kullanacağım. "Basit kapalı bir eğri düzlemi, birini iç, diğerini dışı olarak adlanadırdığımız iki parçaya ayırır , farklı parçalardan alınan noktalar eğriyi kesmeden birleştirilemez, içte veya dışta iki nokta eğriyi kesmeden birleştirilebilir". Bunları Matematik Dünyası dergisi arşivinde
(http://www.matematikdunyasi.org/arsiv/PDF_eskisayilar/1995_3_13_14_AYIRMAK.pdf) bulabilirsiniz.
1. evi A çeşmesine, A çeşmesini 2. eve, 2. evi B çeşmesine ve B çeşmesini 1. eve bağlayan borular düzlemde bir basit kapalı eğri (1A2B1 diyelim) oluşturur. Jordan ın Eğri Teoreminden bu eğri düzlemi (biri içi diğeri dışı olarak adlandırdığımız) iki parçaya ayırır. 3. ev ve C çeşmesinin konumuna göre üç durum vardır:
Biri içte diğeri dıştadır (Çeşme-ev farksız olduğundan birinci durumda hangisi içte hangisi dışta farketmez)
İkisi de içtedir
İkisi de dıştadır.
Biri içte, diğeri dışta ise Jordan eğri teoreminden bunları (Kapalı eğriyi kesmeden) bir yol (boru) ile birleştiremeyiz. Çeliski.
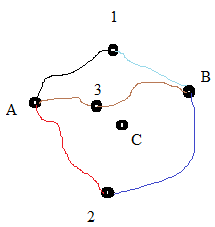
İkisi de içte ise, 3. evi A ve B çeşmelerine bağlayan yolu (boruyu) düşünelim. (borular birbirini kesmediği için) A3B borusu (yolu) 1A2B1 basit kapalı eğrisinin içinde kalır ve onu ikiye ayırır (1A3B1 ve 2A3B2 basit kapalı eğrilerin içleri) . C çeşmesinin bunlardan birinin içinde kalacaktır. C çeşmesinin 2A3B2 basit kapalı eğrisinin içinde varsayabiliriz (yukarıdaki şekle bakın). 1. ev bu eğrinin dışında olduğu için, içteki C çeşmesine bir yol (boru) ile birleştirilmesi (birinici durumdaki gibi) Jordan Eğri Teoremi ile çelişir.
Üçüncü durumda sanırım böyle bir argüment mümkündür, ama daha güzel (geometrik) bir argüment ile bu durumu, ikinci duruma dönüştürebiliriz. 1A2B1 eğrisinin içinden bir P noktası seçelim. Düzleme sonsuzda bir nokta ekleyip küre oluşturalım. Jordan ın Eğri teoremi bu durumda da (tek fark eğrinin içi ve dışını ayırt edemeyiz) geçerlidir. Şimdi 1A2B1 eğrisinin küreyi de iki parçaya ayırır 3. ev ve C çeşmesi aynı parçadadır. Küreden P noktasını çıkadığımızda yine 1A2B1 eğrisi yine (bu yeni) düzlemi de ikiye ayırır ve 3. ev ve C çeşmesi bu kez içerde kalır ve aynı ikinci durumdaki gibi bir çelişki elde ederiz.