Burada sanirim bahsettiginiz iki vektorun ic carpimi (ing. inner product, dot product). Ustune ustluk bu vektorlerin yasadigi uzay da onemli. Eger soyut bir vektor uzayindan bahsediyorsak, bu uzayda bir ic carpim olmak zorunda degil. Hatta ic carpim olan vektor uzaylarina ic carpim uzayi diyoruz. Dolayisiyla sorunun \(\mathbb{R}^n\) uzayindaki standart ic carpim uzerine oldugunu varsayiyorum.
Varsaydigim standartligi biraz daha acalim. Birincisi bu uzaydaki vektorleri \(n\) tane sirali gercel sayi olarak goruyoruz; yani \(v\in\mathbb{R}^n\) aslinda \(\vec{v} = (v_1,\ldots,v_n)\). Ikincisi vektorun uzunlugunu, oklid mesafesinden yola cikarak \(\|\vec{v}\| = \sqrt{v_1^2+\cdots+v_n^2}\) olarak tanimliyoruz. Kokun icindeki ifadeye ihtiyacim olacak, o yuzden ona \(Q(\vec{v}) =v_1^2+\cdots+v_n^2 \) diyelim. Simdi \(\mathbb{R}^n\) uzayindaki standart ic carpimi anlamaya haziriz.
Diyelim ki elimizde iki tane dogrusal bagimsiz vektor var, \(\vec{a},\vec{b}\in\mathbb{R}^n\), ve birinin digeri uzerine dik izdusumunu hesaplamaya calisiyoruz. Vektorlerimiz \(n\) boyutlu olsalar da iki tane dogrusal bagimsiz vektorun dogrusal karisimlarinin uzayi iki boyutlu olacagindan aslinda sorumuzu bir duzleme indirgeyebiliriz. Dolayisiyla resim soyle:
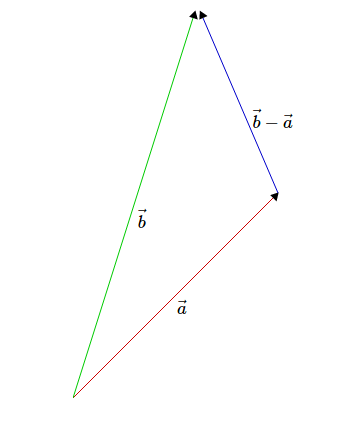
Eger iki vektor arasindaki aciya \(\theta\) dersek, o zaman ucgendeki cosinus formulune gore su cikarimi yapabiliriz.
\[
Q(\vec{b} - \vec{a}) = Q(\vec{a})+Q(\vec{b}) - 2 \|\vec{a}\|\|\vec{b}\|\cos\theta
\]
Simdi, \(\vec{b}\) vektorunun \(\vec{a}\) vektoru uzerine izdusumune \(\vec{v}\) diyelim. O halde,
\[
\|\vec{v}\| = \|\vec a\| \cos\theta \quad\text{ve}\quad \vec{v} = (\|\vec a\| \cos\theta)\frac{\vec{b}}{\|\vec{b}\|}
\]
olur (Burada ikinci esitlikte \(\vec{b}\) yonundeki birim vektoru aldik). Dolayisiyla izdusum icin muhim olan buyukluklerden birisi \(\cos\theta\). Simdi birinci formule donersek
\[
\|\vec{a}\|\|\vec{b}\|\cos\theta = \frac12 \left(Q(\vec{a})+Q(\vec{b}) - Q(\vec{b} - \vec{a})\right)
\]
esitligini cikartabiliriz. Simdi sag tarafi inceleyelim.
\[
\begin{aligned}
Q(\vec{b} - \vec{a}) &= \sum\limits_{i=1}^n (b_i - a_i)^2 \\
&= \sum\limits_{i=1}^n (b_i^2 - 2b_ia_i + a_i^2) \\
&= \sum\limits_{i=1}^n (b_i^2 ) + \sum\limits_{i=1}^n (a_i^2) - 2 \sum\limits_{i=1}^n (b_ia_i)\\
Q(\vec{a}) + Q(\vec{b}) &= \sum\limits_{i=1}^n (b_i^2 ) + \sum\limits_{i=1}^n (a_i^2) \\
\implies Q(\vec{a}) + Q(\vec{b}) - Q(\vec{b} - \vec{a}) &= 2 \sum\limits_{i=1}^n (b_ia_i)
\end{aligned}
\]
Dolayisiyla
\[
\|\vec{a}\|\|\vec{b}\|\cos\theta = \sum\limits_{i=1}^n (b_ia_i)
\]
esitligini elde ediyoruz. Simdi sag tarafin nimetleri buyuk. Eger \(\langle \vec a,\vec b \rangle = \sum\limits_{i=1}^n b_ia_i \) dersek bu tanim her iki girdiye gore dogrusal, ustune ustluk \(Q(\vec{v}) = \langle \vec v, \vec v \rangle\). Izdusumu ise iccarpimi kullanarak
\[
\vec{v} = (\|\vec a\| \cos\theta)\frac{\vec{b}}{\|\vec{b}\|} = \frac{\langle \vec a,\vec b \rangle}{\|\vec b\|}\cdot \frac{\vec{b}}{\|\vec{b}\|} = \frac{\langle \vec a,\vec b \rangle}{\langle \vec b,\vec b \rangle}\vec b
\]
seklinde guzelce yazabiliyoruz. Umarim bu isin sihre benzer tarafini biraz aciklamistir.
Biriciklik guzel bir soru. Cevaba baslarken dedigim gibi ic carpim vektor uzayina eklenen ve bazi ozellikleri saglayan bir yapi. Ozellikler sunlar
\[
\begin{aligned}
\text{(1)}& \langle\cdot,\cdot\rangle \text{ her iki girdiye gore dogrusal ve simetrik}\\
\text{(2)}& \text{ her vektor \(\vec v\) icin} \langle \vec v,\vec v \rangle \geq 0 \text{ oyle ki esitlik sadece ve sadece } \vec v = \vec 0 \text{ ise dogru.}
\end{aligned}
\]
Bu kurallari saglayan baska bir tane ornek verelim. Diyelim ki \(A\) \(n\times n\) simetrik pozitif bir matris (dogrusal donusum dusunmek istersek self-adjoint olmali) olsun ve \(\{\vec{a},\vec{b}\} = \langle \vec{a} , A\vec{b}\rangle\) seklinde olsun. O halde \(\{\cdot,\cdot\}\) (1) ve (2)'yi saglar (guzel bir alistirma). Bunlar fizikte (ozellikle mekanikte) genellestirilmis kutle matrisleri ile bir sistemin enerjisini ifade etmekte kullanilirlar.